Kinds of Infinities

Created: Sat Aug 26, 2023

"Infinity isn't a number." That's the usual response to someone asking a question like "what's zero times infinity?", and... I think it's a bit lacking? It just says that the question is Wrong, but doesn't offer any insight as to why or what a better question might be,

My impression is that those sorts of questions are asked with the belief that somewhere out there in the mathematical universe is this one particular thing bearing the name "infinity", and just saying that this thing is a "concept" instead of a "number" doesn't actually address that belief.

So with that in mind, I'd like to go on a bit of a tour of infinity.

1. Cantor's Candor

If you know a bit about this topic, by now you might have already thought "Of course, infinity isn't a number, Georg Cantor proved there are infinities that are bigger than others!"

And so there we have it! There are multiple infinities, so it can't be a number! But let's take some time to really clarify what this is all about.

Cantor's Theorem deals with what are called cardinal numbers. This is the name for the role a number plays when it's the answer to the question "how many?"

"How many jellybeans are in this jar?" "Fifty two." That's a cardinal number in action.

For questions like "how many whole numbers are there?", "how many fractions are there?", and "how many real numbers are there?" the answer would also be a cardinal number—it just wouldn't be a finite one.

What Cantor proved is there are in fact some infinite sets with more things in them than in others, and therefore there are distinct infinite cardinal numbers. In fact, he proved that for any set, finite or not, its powerset (the set of all its subsets) has a greater cardinality than the original. And since powersets also have their own powersets, you end up with this infinite chain of greater and greater cardinalities.

What's important to point out here is that these infinite cardinals aren't just wild sightings from a trip through math space; they arise from questions about particular objects, and so their behaviours are backed by those of the underlying objects.

For example, it seems reasonable to define that when we merge two sets together, the cardinality of the new one is the sum of those sets' cardinalities. 151 Pokémon in Red and Blue, 100 in the Johto Pokédex, 215 in Gold and Silver's National Pokédex, and therefore 151 + 100 = 251.

Or to say that if we take pairs of things from two sets, then the set of all pairs has a cardinality that is the product of those sets'. 4 suits, 13 values, 52 cards in a standard deck, so 4 × 13 = 52. We use the same idea to work out arithmetic with infinite cardinals.

What's more, since sets on their own don't really have a notion of order, just membership, we can also deduce that addition is commutative: for any two cardinals $x$ and $y$, finite or not, $x+y=y+x$.

But we don't always work with plain old sets. Sometimes we do have other features like order, and have questions about them. To answer those, we'll need a second kind of infinite number.

2. Order in the Court

Sometimes, it's not just how many things we have that's important, but also their order. Which one comes after which, or is bigger than which, that sort of thing. Something's position in an order is also described with a number, and numbers used for this purpose are called ordinals.

You know what else forms a single, increasing chain? The natural numbers!

$$0<1<2<3<...$$

Now how long is this chain? Just like with cardinals, the answer to this would still be a number, it just can't be any of our finite ones. So once again, we can give a name to this new number, the order type of the natural numbers: $\omega$

Why not just reuse ${\mathrm{\aleph }}_0$, if the length of the chain is the same as the number of things in the set? Because with infinite sets, this isn't always the case! Let's take a look at all the set of order types we've seen so far. We've added $\omega$, which is bigger than any finite number:

$$0<1<2<3<...<\omega$$

Remember Hilbert's Hotel? We've added one new thing to an infinite set, so we haven't changed its cardinality: we still have ${\mathrm{\aleph }}_0$ possible lengths. But we have changed the order type. It's not a single increasing chain, with no maximum element. It's a length-$\omega$ chain, followed by a length-1 chain. So it makes sense to call this order type $\omega +1$.

And we can already see a couple of differences between cardinals and ordinals: first, as we just saw, adding 1 gave us a new, distinct order type, even though it did nothing to cardinality. Second, notice how we used $\omega +1$ to mean a chain of length $\omega$, followed by a chain of length 1, where everything in the second chain is greater than everything in the first? What if we do $1+\omega$, the other way around? What if we add a new thing $\alpha$ that's smaller than every natural number?

$$\alpha <0<1<2<...$$

This is actually the same sort of chain as the naturals originally, which you can see by relabelling $\alpha$ to 0 and bumping up the rest of the labels by 1. So $1+\omega$ is actually the same order type as $\omega$ itself! This means $\omega =1+\omega \ne \omega +1$, so unlike cardinals, ordinal addition is not commutative!

If we add in $\omega +1$ to our collection of ordinals, it now looks like this: $$0<1<2<3<...<\omega <\omega +1$$

What's the order type of this? A length-$\omega$ chain, followed by a length-2 chain, why, that's $\omega +2$ of course! And we can just keep going with this, adding $\omega +2$, $\omega +3$, and so on. $$0<1<2<3<...<\omega <\omega +1<\omega +2<\omega +3<...$$

So now we have one $\omega$-length chain, followed by another $\omega$-length chain. That makes this order type, you guessed it, $\omega +\omega$. Alternatively, we took an $\omega$-length chain, and stacked 2 copies of it, so we can also describe it as $\omega \cdot 2$.

This is not to be confused with $2\cdot \omega$, which is a 2-length chain stacked $\omega$ times—that's just $\omega$ again (can you see why?)

And all of these different ordinals are still just ways to arrange a set with ${\mathrm{\aleph }}_0$ elements: we haven't even touched bigger sets here.

One of my favourite applications of infinite ordinals, including ones not covered so far like ${\omega }^4$ (which is still an order for an ${\mathrm{\aleph }}_0$ sized set!) is a couple of papers about infinite chess. Normal chess has mate-in-$n$ puzzles where one side, if they find the right moves, can guarantee that they get checkmate in no more than $n$ moves. These papers describe positions on an infinite chessboard with infinitely many pieces on them where checkmate is still guaranteed, but the opponent can delay it for as long as they want, longer than any finite number of moves, and so you need to bust out the infinite ordinals to describe them.

Now ordinals are pretty fun in their own right (hence this ramble about them), but the reason I bring them up is that not only are they another family of many distinct infinities, but they're a very different kind of object from cardinals. They have different rules of arithmetic because they were made to answer different kinds of questions. To say 'infinity is a concept' and leave it at that doesn't really get across that there are many qualities of objects that might be infinite, and that it's the qualities themselves rather than their finiteness that we care about. Infinite objects of one kind have more in common with their finite counterparts than with other kinds of infinite objects.

And to really stress that, let's take a look at a place where infinity is a number.

3. Take It To The Limit

Despite their differences, the infinite cardinals and ordinals we looked at are both extensions of the natural numbers. They just make a distinction between roles that the finite ones don't need to. So let's shift over from the discrete to the continuous and talk about calculus.

Quick, solve this: $$\underset{x\to \pi }{lim}{x}^2\cos (x)-x$$

Done? No? That's okay. Chances are, your first step was to split up the limit like this: $$[\underset{x\to \pi }{lim}{x}^2]\cdot [\underset{x\to \pi }{lim}\cos (x)]-[\underset{x\to \pi }{lim}x]$$

And don't you think it's kinda weird that you can just... do that? Like, you know those order-of-operations bait posts, the ones that ask things like "what is $8÷2(2+2)$"? Why should switching around the order of taking the limit and doing the arithmetic give you the same answer?

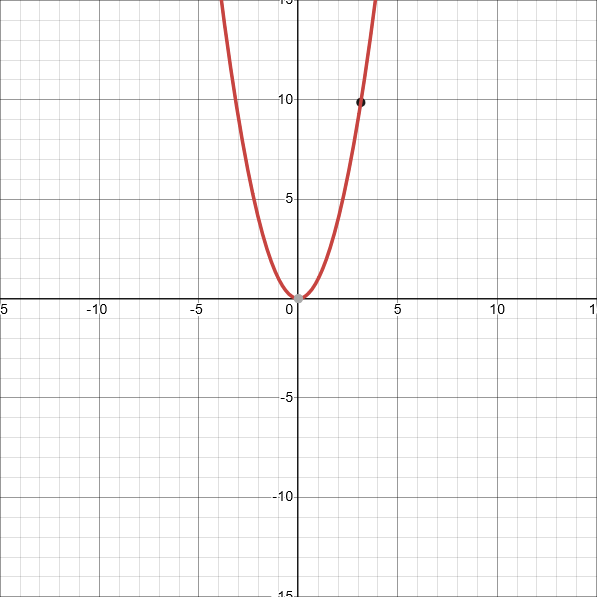
But fortunately for high school students everywhere, we have limit laws like: (assuming all the limits involved exist)

$$\underset{x\to a}{lim}[f(x)+g(x)]=[\underset{x\to a}{lim}f(x)]+[\underset{x\to a}{lim}g(x)]$$ $$\underset{x\to a}{lim}[f(x)\cdot g(x)]=[\underset{x\to a}{lim}f(x)]\cdot [\underset{x\to a}{lim}g(x)]$$ $$\underset{x\to a}{lim}[\frac{f(x)}{g(x)}]=\frac{\underset{x\to a}{lim}f(x)}{\underset{x\to a}{lim}g(x)}\text{ if}\underset{x\to a}{lim}g(x)\ne 0$$

It really should be noted that these limit laws aren't just "to solve your limits homework, replace the left thing with the right thing." These are facts about the objects on either side of the equals sign, statements that they are in fact equal numbers. They aren't definitions, they have to be proven (to the chagrin of people who've taken a calculus class where they had to) by going back to the definition of a limit.

Now here's another limit question:

$$\underset{x\to 0}{lim}\frac{1}{x^2}$$

A quick look at the graph, and your calculus class might say that the limit is infinity.

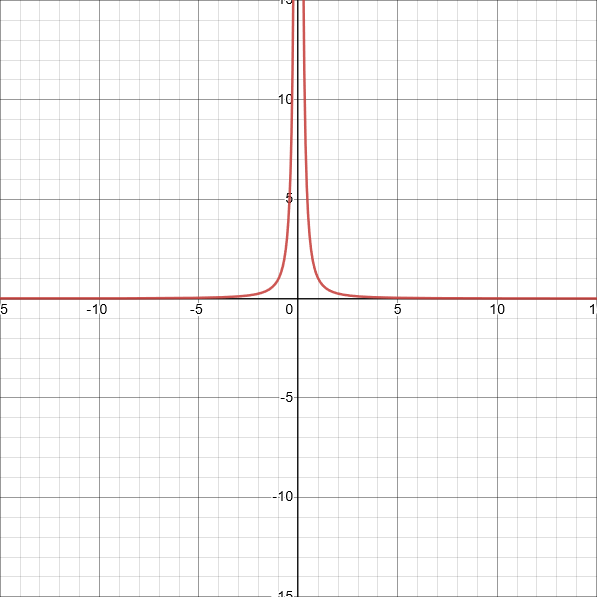
Just one problem: how exactly do you get closer to infinity? Any real number is finite, and therefore infinitely far from infinity.

But also, that graph really makes it look like something's going on. As you get closer to 0 on the x-axis, no matter which side you're on, the output gets bigger and bigger. Is that not, in a sense, getting closer to infinity?

So alright, we can make that a new definition for an "infinite limit": If, as the input to a function gets closer to some point, the output keeps increasing without bound, then the limit of the function at that point is infinity.

The good news is, they're actually pretty compatible with each other, in sensible ways. For example, if $\underset{x\to a}{lim}f(x)$ is a real-valued limit, and $\underset{x\to a}{lim}g(x)$ is an infinite limit, then $\underset{x\to a}{lim}[f(x)+g(x)]$ is also an infinite limit.

We got this new infinity in a similar way as our cardinals and ordinals: we had a question where the answer must be a number, but all the finite ones didn't cut it. We needed to bring in an infinite one to do the job. But this is a very different job, one that normally calls for real numbers in all their continuity instead of the discrete naturals.

4. Beyond

Over the course of procrastinating writing this post, I saw a video on a completely unrelated topic that I felt was making a similar point to what I wanted to get across with this post. It was 12tone's video on whether C♭ and B were the same musical note, where his position was that neither "yes" nor "no" were correct answers. He showed examples of situations where making the distinction was necessary for understanding, and ones where it got in the way. Ultimately, it's applications and concrete questions that matter. Objects like "C♭" exist as part of the models we create to better understand those, and these models contain not just objects but relations and interactions between them.

And it's the same thing here, with the infinities we've covered. The the problem with questions like "what's infinity minus infinity" isn't just that there isn't a single number by that name, or that you can't do arithmetic on a "concept". The problem is that, what would the answer even mean?

If you've been wondering about that question but were never satisfied with the "it's a concept" response, then I hope this post has helped you see some of the really fun mathematics that it was blocking off.